端口视角下的电力系统振荡分析

《浙江电力》约稿论文
更新时间：2024/11/18

研究背景

• 状态空间和传递函数是描述系统动态特性的两个基本方法，前者虽然能够准确描述全部动态，但是依赖于系统完整参数的获得并面临维数灾的问题；后者考察两个物理量之间的传递函数关系，相当于指定了描述系统的一个端口，可通过测量端口物理量获得传递函数关系，工程应用上较为简便。
• 传统电力系统分析中，常用转矩法分析同步电机相关的小信号稳定性，系统被划分为机械部分和电气部分，二者的转矩-转子角/转速传递函数（即转矩系数）构成系统的闭环结构，系统稳定性由两个转矩系数的交互作用决定，重点考察电磁转矩关于角速度的传递函数。
• 新能源电力系统分析中，常用阻抗法分析变流器并网小信号稳定性，源侧和网侧的动态特性分别被压缩至二者在并网点的电压-电流传递函数（即阻抗）中，阻抗之间的关系描述了两侧的交互作用。
• 从形式上看，转矩法和阻抗法都是传递函数方法，然而前者多用于同步电机并网场景，后者多用于变流器并网场景。即目前使用不同的端口分析不同设备的并网稳定性，造成这种差别的原因是什么？

转矩法

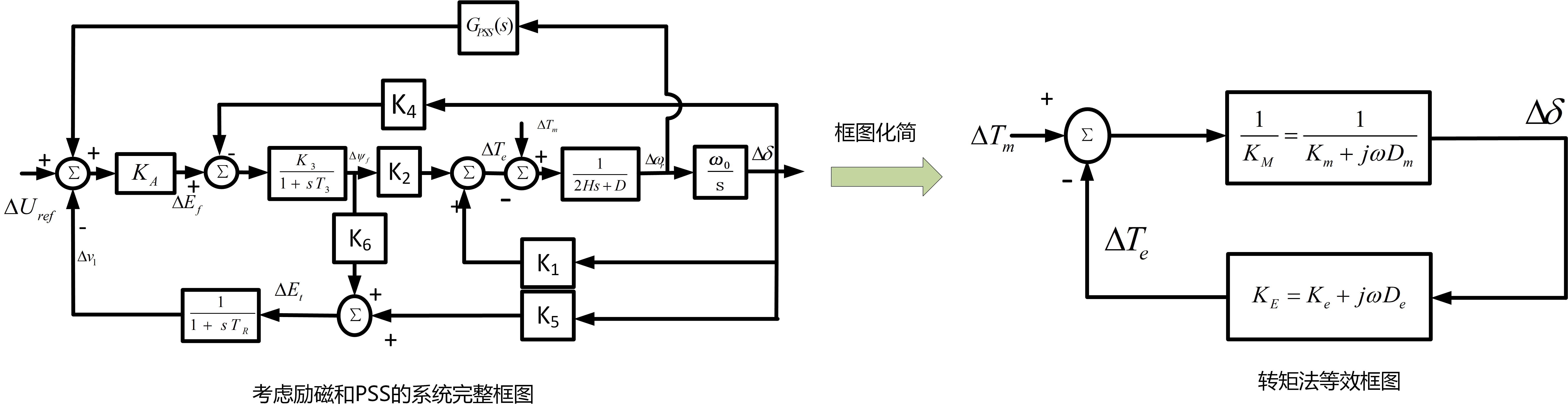
• 复转矩系数法：
  • 将系统框图等效为机械和电气两部分，二者均由转矩系数端口描述；
  • 将转矩关于转子角和转速的传递函数分别定义为同步转矩系数和阻尼转矩系数，同步转矩系数之和为零对应的频率下，若阻尼转矩系数之和小于零则系统不稳定；
  • 该方法可以用牛顿-拉夫逊方法解释数学机理：阻尼转矩系数之和实际上与特征值实部修正量有关，其影响了扰动前后的特征值正负，因此决定了系统稳定性。
• 转矩分量法（阻尼转矩法）：
  • 忽略机械部分，仅考虑电气部分的电气阻尼转矩，以电气阻尼转矩系数的正负作为系统是否稳定的判据；
  • 由于电磁转矩实际中属于制动转矩，因此转矩分量法从物理意义上可以认为是考察发生扰动时系统能否产生正制动转矩阻碍变化以维持稳定；
  • 然而此方法缺乏严格的数学依据，相当于复转矩系数法的简化应用。
• 转矩法的特征：
  • 转矩法物理意义清晰，从阻尼的角度指出了系统稳定性的机理，并且工程应用便捷；
  • 然而，目前转矩法两种主流应用均缺乏严格的数学证明。复转矩系数法将完整框图化简为转矩-转子角/转速的传递函数关系这一步是严格的等效过程，但在处理化简后的框图判稳问题上采用了牛拉法这种数值分析方法，而不是传统控制理论稳定性分析中的奈奎斯特判据或根轨迹等方法。转矩分量法则进一步简化了问题分析，虽然物理意义更明确，但是描述的问题不再严格等价于系统状态空间模型。

阻抗法

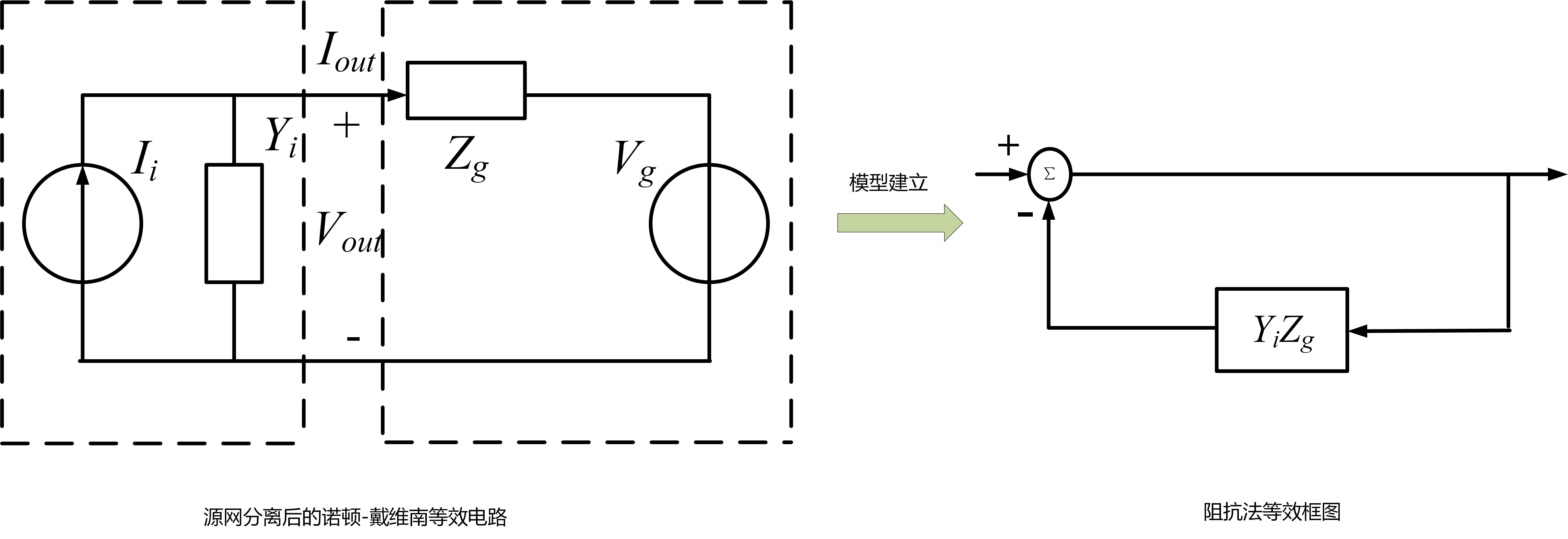
• 序阻抗：
  • 阻抗法将系统阻抗划分为电源侧阻抗以及电网阻抗两部分，分别获得并网点两侧阻抗后，变流器和电网均等效为电源加阻抗的形式，将原先的复杂系统等效为两个电源通过阻抗/导纳交互作用的模型；
  • 序阻抗是指通过谐波线性化方法实现频域的小信号建模，最终获得变流器和电网正序以及负序的等效模型，对阻抗之比使用奈奎斯特判据以及bode图裕度判据等方法可以判断系统稳定性；
  • 这种方法在忽略频率耦合时实现了正负序的解耦，因而判据较为简单。
• dq阻抗：
  • 将三相量经派克变换转换为dq轴上也可以得到稳定的直流工作点，从而进行小信号建模，依托这种思路可以得到变流器和系统的dq阻抗模型；
  • 与序阻抗不同的是，dq阻抗必然是二阶矩阵形式，因此需要使用广义奈奎斯特判据判断系统稳定性。
• 阻抗法的特征：
  • 阻抗模型获得后的系统判稳依赖于奈奎斯特判据等具有严格数学证明的判据；
  • 将系统划分为源侧和网侧，因此并网点两侧的阻抗需要分别测定，通常单一设备的阻抗容易测量，但是网侧的阻抗测量受到多种复杂因素的影响；
  • 有别于转矩法，阻抗法缺乏通过阻尼揭示系统稳定性机理的手段，并且阻抗法认为源网分离的假设是否适用于其他设备并网场景还有待考察。

阻抗法和转矩法的统一性讨论

• 转矩法应用于变流器并网场景：
  • 转矩法从系统阻尼的角度阐释了系统的失稳机理，一个直观的想法是将转矩法应用于变流器并网系统中。同步电机中的转子角自然对应锁相环输出角度，锁相环自身结构与同步电机转子运动方程具有很高的相似性。系统其他环节则理解为附加“转矩”，可以得到具有形式类似性的转矩框图；
  • 应当注意变流器并非旋转设备，因此变流器系统使用转矩法时的“转矩”物理意义不如同步电机中清晰；
  • 传统转矩法的应用常依赖于扫频得到转矩系数，而变流器相关的振荡问题呈现出宽频段特征，故实际应用转矩法也不如同步电机中便捷。

• 阻抗法应用于同步机并网场景：
  • 转矩法在同步电机的次同步振荡分析中已有应用，但在同步电机与电网交互振荡的研究中使用阻抗法较少；
  • 需要注意的是，端口分析方法或者说传递函数分析方法必须与状态空间方法是一致的，端口的获得是基于状态空间框图的化简，得到端口后给出的稳定性判据可能是数值分析方法（转矩法），也可能是准确的频域分析方法（阻抗法）；
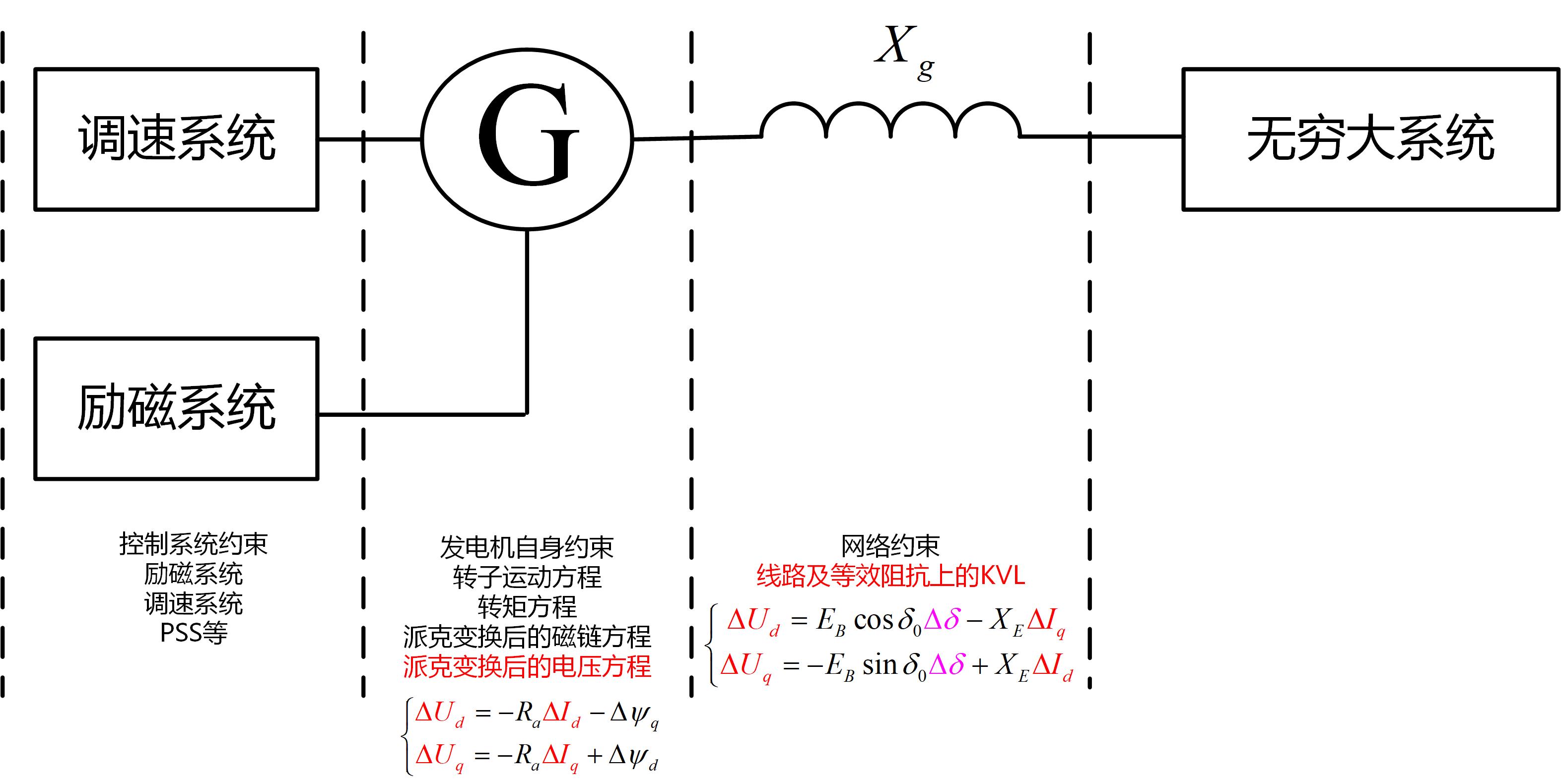
  • 基于上述思路，尝试直接从同步电机系统状态空间模型中得到阻抗端口模型。与电压电流相关的约束方程自然被视作阻抗模型的基础，在同步电机系统状态空间模型中，同步电机派克变换后的电压方程以及网络约束提供了两组电压电流方程，前者可视作同步电机自身的端口阻抗而后者则提供了电网的阻抗，利用状态空间所有方程约去上述两组约束中的其他变量即可得到同步电机的dq阻抗模型，这显然是一个二阶矩阵形式的端口模型，因此需要使用广义奈奎斯特判据判断系统稳定性；
  • 需要注意的是，同步电机并网系统的状态空间方程中，网络约束不只是电压电流变化量之间的关系，转子角的变化量也包含于其中，而转子角由同步电机自身约束决定，因此严格意义上网络等效阻抗与并网设备有关。如果直接忽略掉转子角的变化量，得到的电网阻抗可能导致判稳的不正确，这在一定程度上说明阻抗法认为源网分离并不一定适用于所有设备。按照这个逻辑，阻抗法可以实现变流器厂商和电网只需要分别测量自己端口阻抗模型的优势便不存在了，这里得到的同步电机阻抗端口模型纯粹是状态空间的化简，因此基本只有理论价值。

结论

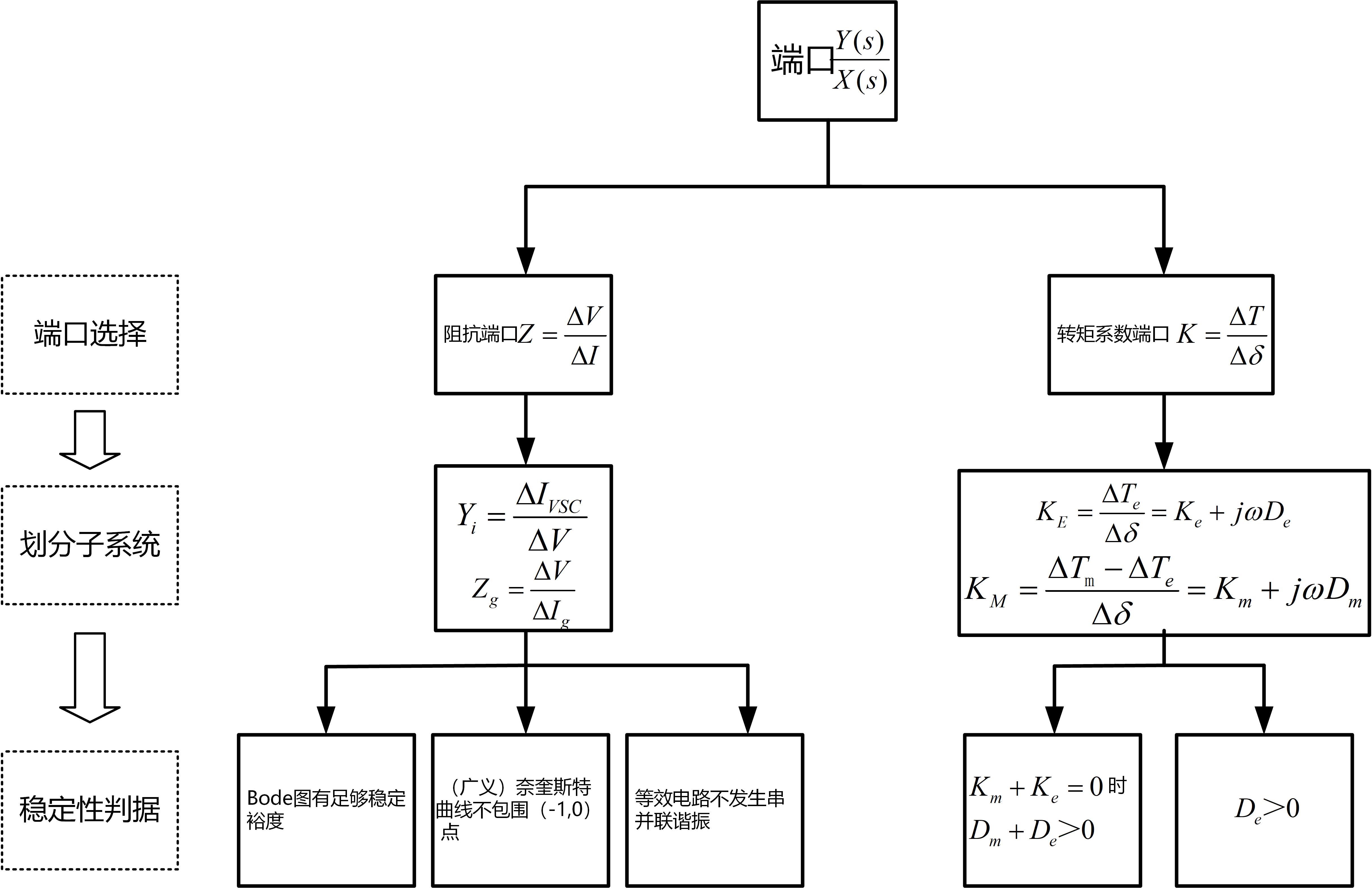
• 端口视角下的电力系统振荡分析大体可以分为两步：端口模型的获得与基于端口模型的稳定性判据，转矩法和阻抗法在这两步均存在不同；
• 转矩法的转矩系数端口是严格的框图化简，然而其稳定性判据是基于物理意义得到，并非严格数学判据。而变流器的阻抗端口基于源网分离的假设而来，其是否是严格的状态空间化简还有待考究，其稳定性判据是严格的；
• 转矩系数端口应用于同步电机并网系统时物理意义清晰，工程应用方便，并且可以分析系统阻尼不足的机理，然而用于变流器并网系统时，由于没有实际转矩，物理意义变弱，宽频带的振荡特征也降低了其应用便捷性；
• 阻抗端口应用于变流器并网系统时将系统划分为两个独立的子系统有利于工程量测，然而这个优势在同步电机系统的实用性尚不明确，并且其难以考察系统稳定机理的缺点使其在可解释性上逊于转矩系数端口；
• 不同端口方法在判断稳定性结果上是一致的，但是实际应用中表现出一定的针对性，阻抗端口更适用于变流器系统，而转矩系数端口更适用于同步电机系统。