Koopman算符理论在新型电力系统分析与控制中的应用与挑战

与清华大学沈沉教授、中国电科院徐式蕴教高联合成果，已被《中国电机工程学报》录用
更新时间：2024/11/12

研究背景

随着新能源电源占比的不断提升，新型电力系统电力电子化的特点日益凸显，系统的稳定基础和控制特性已发生了显著变化，世界范围内新能源电源动态主导的安全稳定事故频发。面对规模巨大、机理复杂的新型电力系统时，“预案式”稳控体系在特性认知依赖系统模型、控制决策依赖运行人员主观经验、安全稳定失配风险加剧等方面的弊端开始显现。

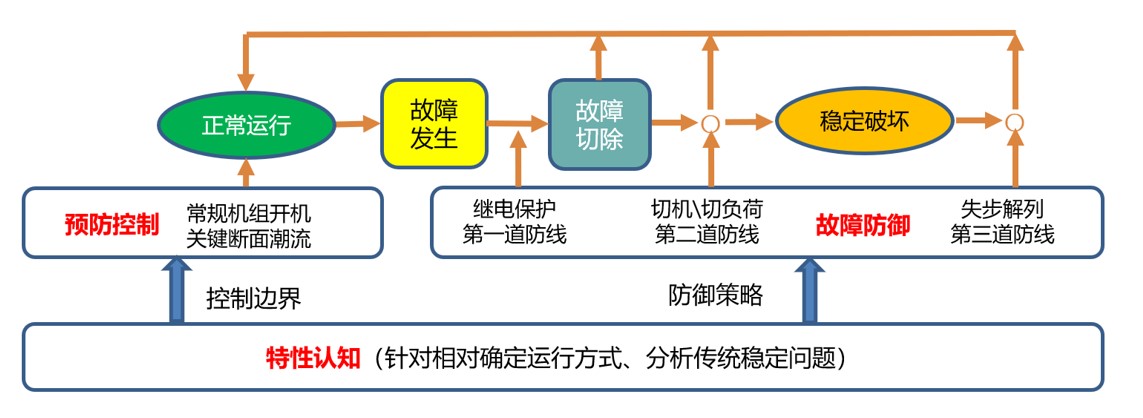
为适应新型电力系统安全稳定运行面临的新挑战，需要建立复杂非线性动力学系统实时判别、实时决策、实时控制的“响应驱动式”分析与控制新范式，回答响应信息对系统特性的可观测性、时变情况下响应信息对系统特性观测的一致性、从响应信息中获取系统可控信息的可行性等一系列科学问题，最终实现复杂大电网安全稳定状态的精准感知、实时评估与最优控制。

作为连接响应信息与复杂非线性系统动态特性的桥梁，Koopman算符使得基于量测数据分析复杂大电网特征成为可能，从而为响应驱动式分析与控制提供了新的研究框架。Koopman算符是一类描述哈密顿动力系统量测量演化的理论，其基本思想是构造线性演化的观察函数观测非线性系统，通过线性系统谱分解完全描述原非线性系统的动态行为，进而实现对非线性动力系统的线性化分析，即利用通用且高效的线性系统分析算法对非线性系统进行辨识、预测和控制。近年来，学术界和工业界对Koopman算符的研究逐渐深入。

Koopman算符的基本性质

线性性质 Koopman算符的线性属性源于观测空间中复合运算的线性。根据Koopman算符的线性性质，任何设计用于线性系统的数学框架都可运用于Koopman算符定义的线性系统，并且通过对该算符研究，可以刻画非线性系统的动力学特征。
谱性质 由于Koopman算符是线性算符，可以对其进行谱分解。由Koopman算符的谱分解可知，特征值能够刻画Koopman模式的时序行为；而Koopman模式仅与观测函数向量以及特征函数相关，且不随状态轨迹而变化，能够描述所关心的观测量在状态空间中的演化特征。

Koopman算符在电力系统中的应用综述

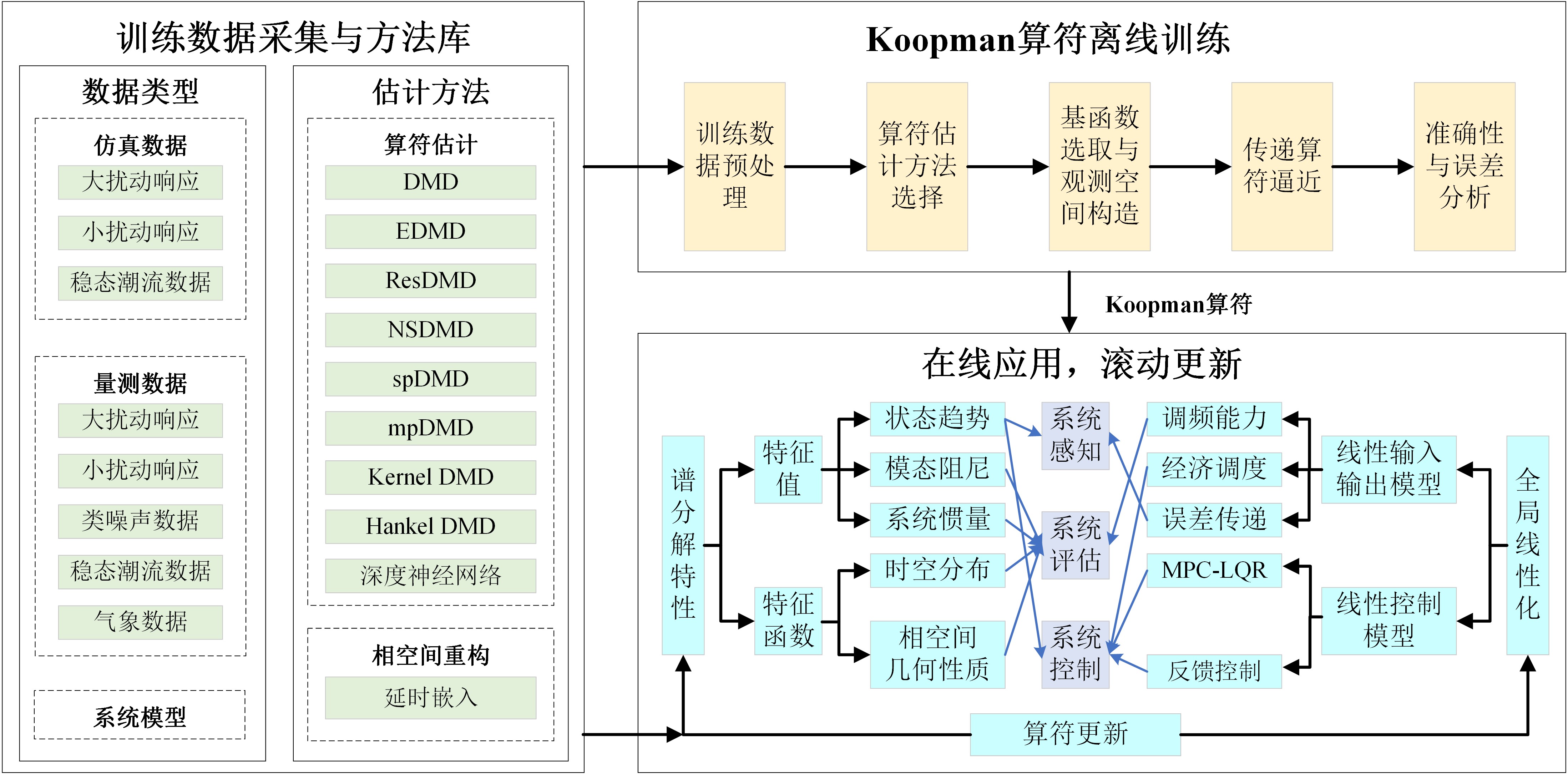
Koopman算符在电力系统中应用的基本思路是“离线训练，在线应用，滚动更新”，其应用方式具有以下几点主要特征：

Koopman算符的应用涵盖了电力系统稳态分析、动态分析、暂态分析等众多应用场景，对资源特征、用户画像、系统响应等特性都能进行刻画，具有良好的应用潜能。
与纯数据驱动模型类似，Koopman算符应用也存在离线训练的过程。训练数据目前主要还是基于系统仿真得到，原因在于电力系统实际运行时的大扰动数据较少，失稳数据几乎没有，则用于系统稳定分析的实际数据较少，这也是纯数据驱动方法面临的问题。
电力系统感知和评估任务中主要应用到了Koopman算符谱分解性质，通过谱特性对系统的特征进行表征，尤其是非线性等传统方法无法挖掘的特征。对应的，控制任务主要应用了算符的线性性质，即将非线性系统线性化之后更有利于系统优化和控制。
Koopman算符是应对新型电力系统“双高”特征的有效工具。一方面，Koopman算符的谱分解性质可用于分析可再生能源本身出力的强不确定性和负荷特征，简化对强不确定性资源的数学描述；另一方面，Koopman算符的线性性质常被用于处理电力电子设备非线性特征。Koopman算符在新能源并网变流器的建模与控制、新能源场站调频能力评估与主动频率支撑、新能源分布式控制等领域已经有了大量应用。

讨论

响应信息对新型电力系统特性的可观性分析 最新的研究给出了基于Koopman算符分析非线性系统可观性判据，另有研究证明了对称非线性系统可观性与Koopman特征值的相似性有关，可用于指导如何选择最小观测集以保证系统完全可观。
响应信息对新型电力系统特性的可控性分析 非线性系统的可控性是另一个值得关注的问题，与可观性类似，经Koopman算符线性化之后系统的可控性也可用于分析原非线性的可控性。新型电力系统实践中，需要更全面地考虑系统的可控性。首先，电力电子电源单机容量小、数量大，单个设备的控制信号通常相对固定，因此挖掘控制敏感的设备和可控范围意义更大。其次，控制代价与场景相关，且还需要综合考虑稳定形态、稳定裕度、响应速度、信号传递等多种因素。同时，电力系统的控制模型不一定能写成控制仿射模型的形式，更一般形式的非线性控制模型的可控性分析有待进一步研究。
新型电力系统响应信息时变性的影响分析 新型电力系统的非自治性更加明显，如故障情况下电力电子设备控制频繁切换，系统动态特性可能发生较大改变。Koopman算符实际应用时，需根据使用场景选择合适的算符估计方法，以平衡算符计算速度、更新速度和估计精度。
响应信息采样时间/空间间隔的影响分析 数据驱动的非线性系统可观/可控性分析还需要考虑响应信息采样间隔对分析结论的影响。一方面，新型电力系统中动态过程的多时间尺度特点突出，对量测信息采样时间间隔的要求需要根据所研究的稳定形态确定。同时，当输入数据包含空间信息时，Koopman算符谱分解中还会包含系统动态的空间频谱，则Koopman算符也可用于分析新型电力系统中频率和电压的空间分布特性，此时对量测装置的空间布点和采样空间间隔亦将有一定要求。

结论

为适应新型电力系统安全稳定运行面临的新挑战，需要建立复杂大电网响应驱动式特性分析和控制新范式。Koopman算符理论可基于量测数据实现非线性系统的全局线性化，为响应驱动的非线性动力系统精准感知、实时评估与最优控制提供了新的研究框架。